How To Make A Pickaxe In Minecraft (All Types)

In this tutorial, you'll learn how to make a pickaxe in Minecraft! In fact, we'll show you how to make all the different types of pickaxes including diamond, iron, stone, wooden, and golden pickaxes!

A Minecraft pickaxe is the most commonly used tool in the game. It's used to mine ores, rock, and blocks at faster speeds.

How To Make Every Pickaxe Video Tutorial

In this video, watch as we show you how to make each type of pickaxe in the game. Plus, we cover some important pickaxe facts and when it's best to use each one.

Available Platforms

Edition	Platform	Available
Java Edition	Windows, Mac & Linux PC's	Yes
Bedrock Edition	Xbox One, Nintendo Switch, iOS, Android, Fire OS, Windows 10 PC's	Yes
Education Edition	Mac, iOs 12, Windows 10 PC's	Yes
PlayStation Edition	PlayStation 3 & 4	Yes

Items Needed To Craft Pickaxes

• 2 Sticks
• 3 planks, cobblestones, iron ingots, gold ingots, OR diamonds

Steps To Craft A Pickaxe

1. Open Your Crafting Menu

First, let's open your crafting menu in Minecraft. You should see the same grid as in the image below.

2. Add Pickaxe Items To The Crafting Table

In the crafting table, add the 2 sticks and depending on the type of pickaxe you want to make, the 3 planks, cobblestones, iron ingots, gold ingots, OR diamonds to the grid.

You must add each item to the crafting grid exactly as shown in the image below. In this example, we will be making a diamond pickaxe.

In the 1st row place down 3 diamonds, one in each box. In the 2nd row place 1 stick in the center box. In the 3rd row place 1 stick in the center box. This is the Minecraft diamond pickaxe recipe. If you want to make a different type of pickaxe, then just replace the diamonds with planks, cobblestones, iron ingots, or gold ingots, depending on the type of pickaxe you want to make.

Now that you've added the items to the crafting grid as described above, you'll notice a diamond pickaxe in the box on the right.

3. Move The Pickaxe To Your Inventory

Simply drag the pickaxe down to your inventory so you can use it.

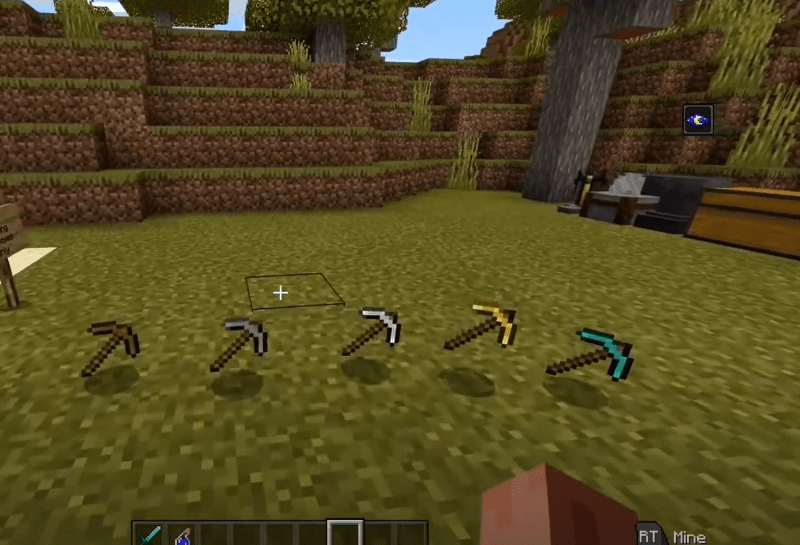
That's it! You now have a pickaxe. A Minecraft pickaxe is the most commonly used tool in the game. It's used to mine ores, rock, and blocks at faster speeds.

Minecraft Pickaxe Command

You can also use a Give Command to create pickaxes in Minecraft. The pickaxe command is available in the following Minecraft editions:

• Java Edition
• Pocket Edition
• Xbox One
• Nintendo Switch
• Windows 10 Edition
• Education Edition

To run the pickaxe command in Minecraft, open your chat window and enter the command below depending on the version you have.

Java Edition 1.13 and higher pickaxe commands

/give @p diamond_pickaxe 1

/give @p iron_pickaxe 1

/give @p stone_pickaxe 1

/give @p wooden_pickaxe 1

/give @p golden_pickaxe 1

PE, Xbox One, Switch, Win 10, Education Edition

/give @p diamond_pickaxe 1 0

/give @p iron_pickaxe 1 0

/give @p stone_pickaxe 1 0

/give @p wooden_pickaxe 1 0

/give @p golden_pickaxe 1 0

More Tool Recipes